Henshin/Examples/DiningPhilosophers

The Dining Philosophers problem is a classical model checking scenario. We use it as an example to give an intuition about the rule-based modeling in Henshin and to conduct a benchmark for its state space exploration feature.

Transformation System

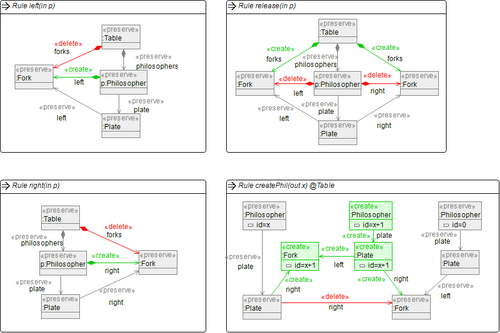
The transformation consists of four rules shown below. In rule left(p) philosopher p picks up his left fork, and analogously for the rule right(p). In rule release(p) the philospher p releases his fork again. The most interesting rule is createPhilosopher(x) where x refers to the highest philosopher ID in the model (note that Henshin can find all parameters automatically here). The rule createPhilosopher(x) can be used to dynamically add a philosopher to the table and to link it to its neighbors. We use this rule to derive initial models for different numbers of philosophers below.

State Space Generation

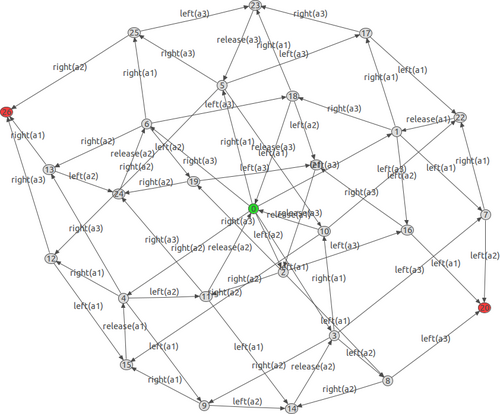
The state space can be either generated in the state space explorer (slow), or by right-clicking on a statespace file and selecting State Space -> Explore State Space, or programmatically as done the DiningPhilsBenchmark class. The screenshot below shows the state space for 3 philosophers as visualized in the state space explorer. Note that we do not make use of graph isomorphy checking for making the state space smaller, because we want to be able to identify each philosopher individually (by its ID).

We conducted a benchmark to measure the speed of the state space generator. The models and the source code for the example can be found here. The following benchmark was conducted on a Intel(R) Xeon(R) CPU @ 2.50GHz with 8GB of main memory using Henshin 0.9.2. We measured the time to generate the full state space.

Philosophers	States (= 3^p)	Transitions	Time
3	27	63	56ms
4	81	252	69ms
5	243	945	224ms
6	729	3,402	616ms
7	2,187	11,907	1.3s
8	6,561	40,824	5.0s
9	19,683	137,781	19.8s
10	59,049	459,270	80.5s
11	177,147	1,515,591	6min
12	531,441	4,960,116	61min
13	1,594,323	16,120,377	593min

contributed by Christian Krause